この記事はhey Advent Calendarの3日目です。
データチームの @komi_edtr_1230 です。
僕はRustが好きで、かつ最近はブロックチェーン周りの技術が楽しくなってきているので、そんなわけで今回のアドベントカレンダーの企画としてRustで公開鍵暗号を実装しました。
データチームはデータ分析の際には個人情報などを取り扱うこともあり、セキュリティについての知識をつけておくのはマストであるので、公開鍵暗号について理解を深めておくのは非常に有用です。
なので今回の記事ではブロックチェーンにも使われている公開鍵暗号の理論的な話、そしてその実装についてまとめていきます。
※説明の中でちょっとだけ算数がありますので算数アレルギーの方はご注意ください。
ブロックチェーンと公開鍵暗号
ブロックチェーンとは何かというと、ネットワークのトランザクションを時系列に沿って保存していくデータ構造です。
ネットワーク内で発生した取引の記録をブロックと呼ばれる記録の塊に格納し、同時にそのブロック内に1つ前に生成されたブロックの内容を示すハッシュ値と呼ばれる情報なども格納するのですが、トランザクションができる度にブロックが時系列的に繋がりながらできていく様子はまさにブロックチェーンというわけです。
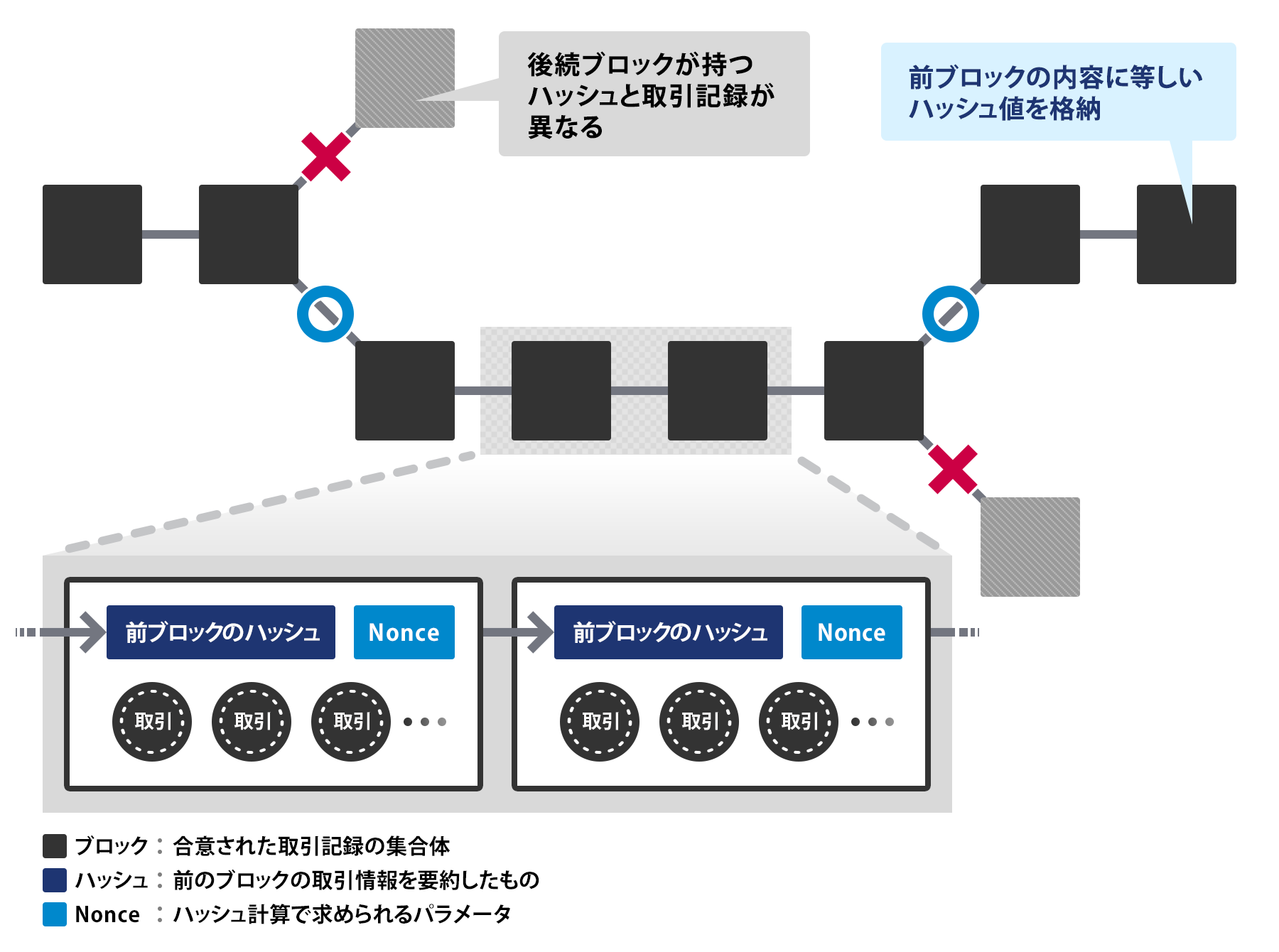 (https://www.nttdata.com/jp/ja/services/blockchain/002/ より)
(https://www.nttdata.com/jp/ja/services/blockchain/002/ より)
ブロックチェーンはデータ構造として比較的単純な様式で連結リストと等価なもののように思えるのですが、ブロックチェーンと連結リストの本質的な違いは署名と検証です。
というのも、ブロックチェーンはビットコインのような通貨を扱うことができる技術であるというのは有名な話ですが、自分が行ったトランザクションを他者が改竄できないようになっているというのが非常に大切なポイントです。
先ほどの説明でブロックチェーン内のブロックにはハッシュ値を格納するという話がありましたが、このハッシュ値をどのように生成することによってトランザクションの中身の正当性が検証可能にできるか、そのためのアプローチが公開鍵暗号です。
公開鍵暗号と楕円曲線暗号
公開鍵暗号とは、ものすごく単純に説明すると、素数を用意して正整数
を
として定義したとき、素数
を知っていれば
を簡単に算出できるけど
だけを知ってるだけでは
が求めるのが大変、みたいな話です。
実際の場合は、暗号文と平文
に対して、鍵
を知っていれば暗号文
と鍵
から平文
を得られるけど、暗号文
だけからは平文
は推測するのが大変という仕組みになっています。
公開鍵暗号というのは基本的にある鍵を知っていれば計算は容易だけどもその鍵が無ければ導出することは困難という特性を使ったもので(一般的にこれは離散対数問題と呼ばれます)、公開鍵暗号というのは色々あり、有名なものとしてはRSA暗号があります。
RSA暗号はどのような機序となっているかというと、ある正整数と素数
を用意し、暗号文
と平文
は以下のように定義されます。
ここでは最大公約数のことです。
一方でビットコインにおいて使われている公開鍵暗号はsecp256k1というもので、楕円曲線暗号の一種です。
楕円曲線とは何かというと
という曲線で、以下のような形をしています(かわいいですね)
(https://ja.wikipedia.org/wiki/%E6%A5%95%E5%86%86%E6%9B%B2%E7%B7%9A より)
先ほどのRSA暗号は一般的な有限体上に定義されたものですが、secp256k1は有限体の演算を楕円曲線に持ち込んだもので、楕円曲線の不思議な性質に基づいて定義されます。
具体的にどのようなものであるかというと、楕円曲線上の点
に対して
を通る直線
を考えた際、
をうまく選ぶことにより直線
は
以外の点
で楕円曲線
と交わるのですが、x軸に対して
と対称な点を
を定義すると(なんとも不思議なことに)楕円曲線上の点の加算は同一性や可換生、結合性、可逆性といった様々な性質を満たすのです。
有限体上での楕円曲線から生成元を取り出すと有限巡回群を構成できるのですが、群は一種類の演算を持ち、楕円曲線暗号ではこの楕円曲線上の点の加法に相当します。
一応この群において単位元はどうなるのかとか完全性はどうなのかといった考えるべきことがたくさんあるのですが、あとはRSAと同じような具合でこの有限巡回群に対して公開鍵暗号のアルゴリズムを構成することができるのです。
ということで早速この楕円曲線暗号をRustで実装していこうと思います。
有限体を実装する
何はともあれ、まずは有限体を実装することから始まります。
有限体は有限個の要素からなる集合と (加法)と
(乗法)が以下を満たす場合と定義されます。
- 集合内の要素
に対し、
と
が共に集合内に存在する
- 集合内の要素
に対し、
のような加法単位元が存在する
- 集合内の要素
に対し、
のような乗法単位元が存在する
- 集合内の要素
に対し、
のような加法逆元が存在する
- 集合内の要素
に対し、
のような乗法逆元が存在する
その上で、位数の有限体の集合を
と表記する場合、以下のように表すことができます。
注意点として、要素は非負整数で位数より小さいものである必要があります。
これをRustで実装すると以下のようになります。
#[derive(Clone, Copy, Debug)] pub struct FieldElement<T> where T: Add<Output = T>, { pub num: T, pub prime: T, } impl<T> FieldElement<T> where T: PartialOrd + Debug + Add<Output = T>, { pub fn new(num: T, prime: T) -> Self { if num >= prime { panic!("Num {:?} not in field range 0 to {:?}", num, prime) } Self { num, prime } } } #[cfg(test)] mod tests { use super::FieldElement; use primitive_types::U256; #[test] fn new() { let _ = FieldElement::new(2, 3); let _ = FieldElement::new(U256::from(2), U256::from(3)); } }
ちなみに今回の記事では最終的にsecp256k1を実装するのですが、secp256k1では256bit整数を取り扱う必要があるのでここでは有限体は要素は型としてprimitive-typesというクレートが提供しているU256というものを利用します。(Rustではネイティブでは128bit整数までしか使えない)
ただ、せっかくRustの素敵な型システムを享受すべく今回の有限体はかなりジェネリックに実装していき、同時にテストもちゃんと書いていきます。テストは大切です。
今回の有限体の要素について、主要な値はその要素の値と有限体の位数で、これを表現するためにRustでは構造体を用います。
せっかくなのでこの有限体の要素を標準出力と等号判定==できるようトレイトを実装していきます。
use std::cmp::{Eq, PartialEq}; use std::fmt::Debug; impl<T> fmt::Display for FieldElement<T> where T: fmt::Display + Add<Output = T>, { fn fmt(&self, f: &mut fmt::Formatter) -> fmt::Result { write!(f, "FieldElement_{}({})", self.prime, self.num) } } impl<T> PartialEq for FieldElement<T> where T: PartialEq + Add<Output = T>, { fn eq(&self, other: &Self) -> bool { return self.prime == other.prime && self.num == other.num; } } impl<T> Eq for FieldElement<T> where T: Eq + Add<Output = T> {} #[cfg(test)] mod tests { use super::FieldElement; use primitive_types::U256; #[test] fn eq() { let a = FieldElement::new(U256::from(2), U256::from(3)); let b = FieldElement::new(U256::from(2), U256::from(3)); let c = FieldElement::new(U256::from(1), U256::from(3)); println!("FieldElement A = {}", a); assert_eq!(a, b); assert_ne!(a, c); } }
さて、次に有限体の演算ですが、ひとまず加算について考えます。
有限体の集合について、加算は閉じている(要素同士の加算の結果も有限体の集合内に存在している)必要があるのですが、ここはモジュロ演算によってこの性質を保証することができます。
つまりどういうことかというと、有限体の要素についての加算を基本的にで割った余りとして扱うことで集合内で閉じるようにさせます。
ここでを有限体上の加算の記号としました。
具体的に、位数の有限体で要素
の加算の結果は
、つまり
となります。
これを実装しましょう。
impl<T> Add for FieldElement<T> where T: PartialEq + Add<Output = T> + Sub<Output = T> + PartialOrd + Debug + Copy, { type Output = Self; fn add(self, other: Self) -> Self::Output { if self.prime != other.prime { panic!("Prime number should be same") } if self.num + other.num >= self.prime { Self::new(self.num + other.num - self.prime, self.prime) } else { Self::new(self.num + other.num, self.prime) } } } #[cfg(test)] mod tests { use super::FieldElement; use primitive_types::U256;= #[test] fn add() { let a = FieldElement::new(U256::from(2), U256::from(7)); let b = FieldElement::new(U256::from(1), U256::from(7)); let c = FieldElement::new(U256::from(3), U256::from(7)); assert_eq!(a + b, c); } }
Addトレイトを実装することでFieldElement型同士の+が使えるようになりました。
ポイントとして+が使えるのはそれぞれの有限体の位数が同じ場合であり、これが異なる場合はpanicさせます。
加算ができるようになると減算がしたくなるのが人間です。 お察しの通り減算も同様にモジュロ演算で、引き算の結果がマイナスになるこれも実装しましょう。
impl<T> Sub for FieldElement<T> where T: PartialEq + Add<Output = T> + Sub<Output = T> + PartialOrd + Debug + Copy, { type Output = Self; fn sub(self, other: Self) -> Self::Output { if self.prime != other.prime { panic!("Cannot subtract two numbers in different Fields."); } if self.num < other.num { Self::new(self.prime + self.num - other.num, self.prime) } else { Self::new(self.num - other.num, self.prime) } } } #[cfg(test)] mod tests { use super::FieldElement; use primitive_types::U256; #[test] fn sub() { let a = FieldElement::new(U256::from(6), U256::from(7)); let b = FieldElement::new(U256::from(4), U256::from(7)); let c = FieldElement::new(U256::from(2), U256::from(7)); assert_eq!(a - b, c); } }
ワクワクしてきましたね。
さて、次に乗算ですがこれは簡単で、
このように乗算は加算として解釈が可能です。
これもサクッと実装しましょう。
impl<T> Mul for FieldElement<T> where T: PartialEq + Add<Output = T> + Sub<Output = T> + Div<Output = T> + PartialOrd + Debug + Copy, { type Output = Self; fn mul(self, other: Self) -> Self { if self.prime != other.prime { panic!("Cannot multiply two numbers in different Fields."); } let zero = self.prime - self.prime; let one = self.prime / self.prime; let mut counter = other.num; let mut ret = FieldElement::new(zero, self.prime); while counter > zero { ret = ret + self; counter = counter - one; } ret } } #[cfg(test)] mod tests { use super::FieldElement; use primitive_types::U256; #[test] fn mul() { let a = FieldElement::new(3, 13); let b = FieldElement::new(12, 13); let c = FieldElement::new(10, 13); assert_eq!(a * b, c); } }
この実装で複数回加算をしてあげればいいのでwhile文を回せば良いのですが、カウンター変数を操作したり状態確認するために0や1といったジェネリック型ではない数字を持ち出す必要があり、現行のRustではnum::Oneやnum::Zeroといったトレイトは廃止されてしまっているので利用できず、かつFromトレイトでT::from(0)というのは型エラーとなってしまうので
let zero = self.prime - self.prime; let one = self.prime / self.prime;
というような方法でトレイト境界内で実現しました。
次に除算ですが、例えばというのは
と等価です。
つまりは有限体の集合では何になるかを考えれば良いのですが、ここでフェルマーの小定理を持ち出します。
フェルマーの小定理とは以下のようなstatementです。
この定理は大学受験レベルの数学で簡単に証明できるので割愛しますが、この事実を使うことによって
として解釈でき、結論として
となります。
つまり除算の定義は乗算と冪乗だけで再定義できるのです。
impl<T> Div for FieldElement<T> where T: Add<Output = T> + Mul<Output = T> + Sub<Output = T> + Div<Output = T> + Rem<Output = T> + PartialOrd + Debug + Copy, { type Output = Self; fn div(self, other: Self) -> Self { let p = self.prime; let one = self.prime / self.prime; self * other.pow(p - one - one) } } impl<T> FieldElement<T> where T: Add<Output = T> + Mul<Output = T> + Sub<Output = T> + Div<Output = T> + Rem<Output = T> + PartialOrd + Debug + Copy, { fn pow(self, exponent: T) -> Self { let zero = self.prime - self.prime; let one = self.prime / self.prime; let mut ret = FieldElement::new(one, self.prime); let mut counter = exponent % (self.prime - one); while counter > zero { ret = ret * self; counter = counter - one; } ret } } #[cfg(test)] mod tests { use super::FieldElement; use primitive_types::U256; #[test] fn pow() { let a = FieldElement::new(U256::from(3), U256::from(13)); let b = FieldElement::new(U256::from(1), U256::from(13)); assert_eq!(a.pow(U256::from(3)), b); } #[test] fn div() { let a = FieldElement::new(U256::from(7), U256::from(19)); let b = FieldElement::new(U256::from(5), U256::from(19)); let c = FieldElement::new(U256::from(9), U256::from(19)); assert_eq!(a / b, c); } }
これにて有限体とその演算が実装できました。
有限体上の楕円曲線
楕円曲線は先述した通りy2=x3 + ax + bという数式によって表現される曲線です。
楕円曲線暗号はこの点についての演算を考えるのですが、楕円曲線上の点
に対して
を通る直線
を考えた際、
をうまく選ぶことにより直線
は
以外の点
で楕円曲線
と交わるのですが、x軸に対して
と対称な点を
として定義します。
この点の加法は、単位元を無限遠点とすることによって先ほど有限体の性質として見た同一性や結合性、可換性、可逆性を満たすのです。
実際、点の加法は各点を通る直線を考えるので、楕円曲線との交点を考えれば比較的自然と納得いくと思います。(ちゃんと数学をやっている人から怒られてしまいそうですが)
ということで、これを実装します。
まず、楕円曲線上の点については以下のように定義できます。
// Elliptic Curve: y^2 = x^3 + a*x + b #[derive(Clone, Debug)] pub enum Point<T> { Coordinate { x: T, y: T, a: T, b: T }, Infinity, } impl<T> fmt::Display for Point<T> where T: fmt::Display, { fn fmt(&self, f: &mut fmt::Formatter) -> fmt::Result { match &self { &Point::Coordinate { x, y, a, b } => { write!(f, "Point({}, {})_{}_{}", x, y, a, b) } &Point::Infinity => { write!(f, "Point(infinity)") } } } } impl<T> Point<T> where T: Add<Output = T> + Mul<Output = T> + PartialEq + Copy, { pub fn new(x: T, y: T, a: T, b: T) -> Self { if y * y != x * x * x + a * x + b { panic!("This is invalid number."); } Self::Coordinate { x, y, a, b } } } #[cfg(test)] mod tests { use super::*; use primitive_types::U256; #[test] fn new() { let _ = Point::new(U256::from(18), U256::from(77), U256::from(5), U256::from(7)); } #[test] fn eq() { let a = Point::new(U256::from(18), U256::from(77), U256::from(5), U256::from(7)); let b = Point::new(U256::from(18), U256::from(77), U256::from(5), U256::from(7)); assert!(a == b); } }
実際の点か無限遠点かで2パターンあるのでenumを利用します。
次に、点の加算ですが、これは普通に2点を通る直線をとってその楕円曲線との交点を考えて...と普通に実装すればOKです。
impl<T> Add for Point<T> where T: PartialEq + Add<Output = T> + Sub<Output = T> + Div<Output = T> + Mul<Output = T> + Copy, { type Output = Self; fn add(self, other: Self) -> Self { use Point::*; match (self, other) { ( Coordinate { x: x0, y: y0, a: a0, b: b0, }, Coordinate { x: x1, y: y1, a: a1, b: b1, }, ) => { if a0 != a1 || b0 != b1 { panic!("Points are not on the same curve.") } if x0 == x1 { if y0 == y1 - y1 { return Infinity; } let one = a0 / a0; let two = one + one; let three = one + one + one; let s = (three * x0 * x0 + a0) / (two * y0); let x2 = s * s - two * x0; return Coordinate { x: x2, y: s * (x0 - x2) - y0, a: a0, b: b0, }; } let s = (y1 - y0) / (x1 - x0); let x2 = s * s - x1 - x0; let y2 = s * (x0 - x2) - y0; return Coordinate { x: x2, y: y2, a: a0, b: b0, }; } (Coordinate { x, y, a, b }, Infinity) => Coordinate { x, y, a, b }, (Infinity, Coordinate { x, y, a, b }) => Coordinate { x, y, a, b }, (Infinity, Infinity) => Infinity, } } }
ポイントとして、加算の対象が無限遠点の場合、2点間の直線は垂直線となるので加算の結果は元の点のままです。同一性ですね。
さて、この楕円曲線の点の加算ですが、実は有限体上でもちゃんと同様に加算ができるのです! なんとも不思議な感じがしますね!
実際に動かしてみましょう。
#[cfg(test)] mod tests { use super::*; use primitive_types::U256; #[test] fn point_on_elliptic_curve() { let a = FieldElement::new(U256::from(0), U256::from(223)); let b = FieldElement::new(U256::from(7), U256::from(223)); let x = FieldElement::new(U256::from(192), U256::from(223)); let y = FieldElement::new(U256::from(105), U256::from(223)); assert_eq!(y * y, x * x * x + a * x + b); } #[test] fn add_points() { let a = FieldElement::new(U256::from(0), U256::from(223)); let b = FieldElement::new(U256::from(7), U256::from(223)); let x0 = FieldElement::new(U256::from(192), U256::from(223)); let y0 = FieldElement::new(U256::from(105), U256::from(223)); let x1 = FieldElement::new(U256::from(17), U256::from(223)); let y1 = FieldElement::new(U256::from(56), U256::from(223)); let x2 = FieldElement::new(U256::from(170), U256::from(223)); let y2 = FieldElement::new(U256::from(142), U256::from(223)); let p0 = Point::new(x0, y0, a, b); let p1 = Point::new(x1, y1, a, b); let p2 = Point::new(x2, y2, a, b); assert_ne!(p0, p1); assert_eq!(p0 + p1, p2); } }
実際に動いています!すごいですね!
楕円曲線暗号
普通のアドベントカレンダーの一記事としてはおかしすぎるだろというような記事の重さになってきた気がしますが、あともうひと踏ん張りです。
ここまでで有限体とその上で動く楕円曲線を作りましたが、先ほど作ったのは楕円関数上の点の加法だけでした。
この加法を拡張して、というようにスカラー倍算を考えます。
一旦これを実装しましょう。
impl<T, U> Mul<U> for Point<T> where T: Add<Output = T> + Sub<Output = T> + Div<Output = T> + Mul<Output = T> + PartialOrd + Copy, U: Sub<Output = U> + Div<Output = U> + Mul<Output = U> + PartialOrd + Copy, { type Output = Point<T>; fn mul(self, other: U) -> Self::Output { let zero = other - other; let one = other / other; let mut counter = other; let mut ret = Self::Infinity; while counter > zero { ret = ret + self; counter = counter - one; } ret } } #[cfg(test)] mod tests { use super::*; use primitive_types::U256; #[test] fn mul() { let p0 = Point::new(2, 5, 5, 7); let p1 = Point::new(2, -5, 5, 7); assert_ne!(p0, p1); assert_eq!(p0 * 3, p1); assert_eq!(p0 * U256::from(3), p1); } }
ここではジェネリクス型としてPoint<T>とは異なるUを用いることにより、点のスカラー倍算が様々な型でも計算ができるようにしておきました。
この点のスカラー倍算の特徴として、ある乗算によって点は無限遠点になります。
つまり、ある整数に対して生成元
は
となります。
(ここで無限遠点は加法単位元であり0と表しました)
結果的にスカラー倍算は
この群は有限体で見たように同一性や可換性、結合性や可逆性を持ちます。
さて、ここまで長い旅を続けてきましたが、おかげでようやく公開鍵暗号の演算をするのに必要なツールが揃いました。
- 楕円曲線の係数
- 有限体の位数
- 生成元となる点
の座標
により生成される群の位数
今までは一般的な有限体と楕円曲線について実装を進めていきましたが、ここで実装する公開鍵暗号はsecp256k1を利用するので、楕円曲線はy2=x3 + 7とし、他のパラメータも以下のようにします。
- a=0, b=7
- p=0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
- x=0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
- y=0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8
- n=0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
この点が楕円曲線上にあることを確認しましょう。
#[cfg(test)] mod tests { use super::*; use primitive_types::{U256, U512}; #[test] fn on_the_curve() { let p = U512::from_str_radix( "FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F", 16, ) .unwrap(); let x = U512::from_str_radix( "79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798", 16, ) .unwrap(); let y = U512::from_str_radix( "483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8", 16, ) .unwrap(); let n = U512::from_str_radix( "FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141", 16, ) .unwrap(); let a = FieldElement::new(U512::from(0), p); let b = FieldElement::new(U512::from(7), p); let gx = FieldElement::new(x, p); let gy = FieldElement::new(y, p); let _ = Point::new(gx, gy, a, b); } }
今回は記事の執筆の都合でU256の型以内で演算を完結させるのが大変だったため、ここは簡便にU512型を使います。
公開鍵暗号は、整数と楕円曲線による有限巡回群の生成元
に対して
として表現されます。
これは、有限体における楕円曲線では点の加算の結果は規則性がないため、
を知っていても
を推測することは難しいという特性を利用しています。
逆に、
を知っていれば
が成立することを簡単に確認できます。
ここでが秘密鍵、
が公開鍵です。
署名と検証のアルゴリズムは、ランダムな整数と署名ハッシュ
、秘密鍵
として公開鍵は以下のように表されます。
ここで署名をとします。これは本質的には
の式と等価で、署名ハッシュと署名を知っていれば検証ができるし秘密鍵を作れば公開鍵を作ることができます。
それでは最後にこれを実装します。
use sha2::Sha256; fn make_hash(source: &[u8]) -> U512 { let mut hasher = Sha256::new(); hasher.update(source); U512::from(&hasher.finalize()[..]) } // 署名ハッシュ作成 let z = FieldElement::new(make_hash(b"This is my sign"), n); // 秘密鍵作成 let e = FieldElement::new(make_hash(b"This is my secret"), n); // 乱数kを生成 use rand::Rng; let mut rng = rand::thread_rng(); let i: i32 = rng.gen(); let k = FieldElement::new(U512::from(rng.gen::<i32>()), n); let G = Point::new(gx, gy, a, b); let r = (G * k).x; let k_inv = FieldElement::new(k, n).pow(n-U512::from(2)); let s = (z + r * e) * k_inv; let P = G * e;
これにて公開鍵を作成することができました。 これは容易に署名を用いて検証することができます。
終わりに
今回はRustを用いて公開鍵暗号を作成しました。 代数学における基本的な操作からこのような複雑な暗号が作り出せると思うと非常にワクワクしますね。
heyのデータチームではデータ分析において客観性や再現性などサイエンス的な視点を重要視しており、統計モデリングや実験計画法など数理的な概念をたくさん使用して普段から業務を行なっています。 そのため数理的なディスカッションも多々あります!
データチームでは数理的な思考に強みがあるデータアナリストを募集しています!
We are hiring !

